NCERT Solutions for Class 10 Maths Chapter 2 Polynomial

Children, if you are a class 10 student then learnbseb.in has brought for you NCERT Solutions for Class 10 Maths Chapter 2 Polynomial so that you can prepare well for 10th Class 10 maths chapter 2 by BSEB teacher

Class 10 maths chapter 2 exercise 2.1

Class 10 maths chapter 2 exercise 2.2

Class 10 maths chapter 2 exercise 2.3

Class 10 maths chapter 2 exercise 2.4

In all these chapters, one will get to read about the types of polynomials and polynomials. Constant Polynomial, Linear Polynomial, Quadratic Polynomial

It has been told about the relation between the quadratic polynomial  and the zeros and zeroes of the polynomial,

and how many zeroes there will be in any graph maths chapter 2 exercise 2.1 and Know the zeroes of the polynomials and the difference between the zeroes and the coefficients

You will learn to check the veracity of the relationship In 10 maths chapter 2 exercise 2.2 and by using a division algorithm, we will learn to find the quotient and remainder when p(x) is divided by g(x) and find the zero by factoring it in 10 maths chapter 2 exercise 2.3 and you will learn

In 10 maths chapter 2 exercise 2.4, verify that the given numbers with the following quadratic polynomials have their zeroes.  also learn to verify the relationship between the zeroes and the coefficients in each case

b + b₁x  + b₂x²  +  b₃x³ +……………… + b_nxⁿ  के  जैसे  रहने  वाले  व्यंजक  को  बहुपद  कहते  है।जहाँ b , b₁ , b₂ , b₃  …… b_n  अचर  वास्तविक संख्याएँ  है तथा n प्राकृतिक संख्या होगा ।तथा x का घात भी प्राकृतिक होगा जैसे  – 7x⁵ + 4x³ + 6x²

बहुपदो को घात के  आधार  पर  निम्न वर्गों  में विभाजित किया गया  है  जो इस प्रकार है

1.अचर बहुपद (  constant Polynomial )

2.रैखिक बहुपद ( Linear  Polynomial )

3.द्विघात बहुपद   ( Quadratic Polynomial)

4.त्रिघात बहुपद (Cubic  Polynomial )

1.अचर बहुपद (constant  Polynomial )

यदि किसी बहुपद का घात शून्य हो उसे अचर बहुपद कहते है

p(x) =  2  को अचर बहुपद कहते है इस बहुपद का  घात  शून्य होता  है

2.रैखिक बहुपद  (Linear Polynomial )

यदि किसी बहुपद  के सिर्फ एक घात होते है  वैसे   बहुपद , रैखिक बहुपद  कहते है

उदाहरण:-  ax + b, जहाँ a, b वास्तविक संख्या है और    a ≠ 0

3.द्विघात बहुपद   (Quadratic Polynomial )

यदि किसी  बहुपद के  दो घात होते है  वैसे बहुपद , द्विघात बहुपद कहलाते  है

उदाहरण:- ax² + bx + c,   जहाँ  a,b ,c वास्तिविक संख्या है और a ≠ 0 यह एक  द्विघात बहुपद है

4. त्रिघात बहुपद  ( Cubic  Polynomial )

वैसे बहुपद जिसके तीन घात होते है उस बहुपद को   त्रिघात बहुपद कहते है

उदाहरण:- ax³ + bx² + cx + d जहाँ   a,b,c,d, वास्तविक संख्या है और a ≠ 0 यह एक   त्रिघातीय बहुपद है

पद के आधार पर बहुपद को निम्न प्रकार में विभाजित किया गया है जो इस प्रकार है।

1.एकपदी बहुपद ( Monomial )

2.द्विपदी बहुपद ( Binomial )

3.त्रिपदी बहुपद ( Trinomial )

1.एकपदी बहुपद ( Monomial )

यदि बहुपद का एक  ही पद  हो उस बहुपद को  एकपदी बहुपद कहते है

उदाहरण:- 3, x, y² आदि.

2.द्विपदी बहुपद ( Binomial )

यदि बहुपद का दो पद हो उस   बहुपद को द्विपदी  बहुपद कहते है

उदाहरण:- x + 2, x – 6, x² + 2, x – 6  आदि

3.त्रिपदी  बहुपद  ( Trinomial )

यदि बहुपद का तीन पद हो वैसे   बहुपद  को  त्रिपदी बहुपद कहते है

उदाहरण:- 2x² + 9x + 5 , x³ + 5x² – 3x

बहुपद का शून्यक  ( Zeroes of Polynomial )

किसी बहुपद के चार के लिए सभी मान जो बहुपद को शून्य  कर दे, उसे बहुपद का  शून्यक  कहा जाता है

उदाहरण:-ax + b का  शून्यक  – b / a  होता है

सारांश

1.  चर x के बहुपद p(x) में x की उच्चतम घात पहुपद की घात कहलाती है
2.  रैखिक बहुपद  ax+b ,a ≠ 0 के लिए Y =ax+ b का सरल रेखा है जो X अक्ष को ठीक एक बिंदु पर प्रतिच्छेद करती है और  रैखिक बहुपद के सिर्फ एक शुन्यक होगा
3. द्विघात बहुपद  X अक्ष को ठीक दो  बिंदु पर प्रतिच्छेद करती  है और इसके दो शून्यक होते है
4. द्विघात बहुपद  ax²+bx+c ,a ≠ 0 का ग्राफ परवलय होता है और परवलय ऊपर की ओर होगा या नीचे की ओर यह निर्भर करता है a>0 या a<0
5. द्विघात बहुपद के अधिकतम दो शून्यक हो सकते है।
6. त्रिघात बहुपद के अधिकतम तीन शून्यक होते है और यह  x अक्ष को तीन बिंदु पर प्रतिच्छेद करती है

बहुपद के शून्यको और गुणांको में संबंध

1. रैखिक बहुपद ax+b का शून्यक -b/a  होता हैं
2. द्विघात बहुपद ax²+bx+c के शून्यक α और β हो तो  α+β=  -b/a,     αβ=   c/a
3.  यदि α,β,γ त्रिघात बहुपद ax³ +bx² +cx+d=0 के शून्यक हो तो

        α+β+γ = -b/a

       αβ+βγ +γα = c/a

       αβγ = -d/a

Class 10 maths chapter 2 exercise 2.1

 प्रश्नावली 2.1

 1. किसी बहुपद p (x) के लिए ग्राफ y = p (x) का ग्राफ नीचे आकृति में दिया है प्रत्येक स्थिति में p(x)  के शुन्यको की संख्या ज्ञात कीजिए।

(I)

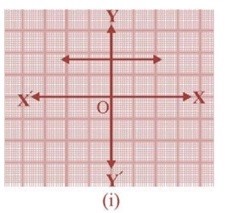
इस ग्राफ में रेखा  x अक्ष को नही कट कर रहा है इसलिए इसका कोई शून्यक नही होगा

P (x) की शून्यक =0

(II)

इस ग्राफ में रेखा  x अक्ष को एक बार कट कर रहा है इसलिए इसका एक शून्यक  होगा ।

P (x) की शून्यक =1

(III)

इस ग्राफ में रेखा  x अक्ष को तीन बार कट कर रहा है इसलिए इसका तीन शून्यक  होगा ।

P (x) की शून्यक =3

(IV)

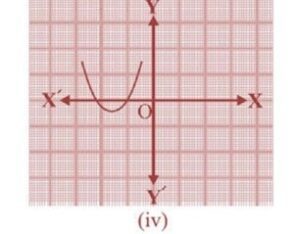
इस ग्राफ में रेखा  x अक्ष को दो बार कट कर रहा है इसलिए इसका दो शून्यक  होगा ।

P (x) की शून्यक =2

(V)

इस ग्राफ में रेखा  x अक्ष को चार बार कट कर रहा है इसलिए इसका चार शून्यक  होगा ।

P (x) की शून्यक =4

(VI)

इस ग्राफ में रेखा  x अक्ष को तीन  बार कट कर रहा है इसलिए इसका तीन शून्यक  होगा ।

P (x) की शून्यक =3

Class 10 maths chapter 2 exercise 2.2

प्रश्नावली 2.2

1. निम्न द्विघात  बहुपदों के शून्यक ज्ञात कीजिए और शून्यको तथा गुणांको के बीच के संबंध की सत्यता की जांच कीजिए  :
   1. 1. x² +2x-8
      2. 4s²-4s+1
      3. 6x²-3-7x
      4. 4u²+8u
      5. t²-15
      6. 3x²-x-4

(i) x² +2x-8

हल:

x² +2x-8=0

x²+4x-2x-8=0

x(x+4)-2(x+4)=0

(x-2)(x+4)=0

अतः (x -2)=0 और (x+4)=0

x =2  और x= – 4

x का दो शून्यक α = 2 और β= -4

शून्यको तथा गुणांको के बीच के संबंध की सत्यता की जांच

a = 1    b = 2     c = -8

शून्यको का योग (α+β)=   -b/a

(2+-4)= -2/1

-2=-2

शून्यको का गुणनफल (αβ)=   c/a

(2*-4)= -8/1

-8=-8

दोनो स्थितियों में संबंध सत्य है

(ii) 4s²-4s+1

हल:

4s²-4s+1=0

4s²-2s-2s+1=0

2s(2s-1)-1(2s-1)=0

(2s-1)(2s-1)=0

अतः (2s-1)=0 और (2s-1)=0

S=½ और s=½

S का दो शून्यक α = ½ और β= ½

शून्यको तथा गुणांको के बीच के संबंध की सत्यता की जांच

a = 4   b = – 4     c = 1

शून्यको का योग (α+β)=   -b/a

(½+½)= -(-4)/4

2/2= 4/4

1=1

शून्यको का गुणनफल (αβ)=   c/a

(½*½)=¼

¼ =¼

दोनो स्थितियों में संबंध सत्य है

(iii) 6x²-3-7x

हल:

6x²-3-7x=0

6x²-7x-3=0

6x²-9x+2x-3=0

3x(2x-3) +1(2x-3)=0

(3x+1)(2x-3)=0

अतः(3x+1)=0और (2x-3)=0

X= -⅓  or x = 3/2

x का दो शून्यक α = -⅓ और β= 3/2

शून्यको तथा गुणांको के बीच के संबंध की सत्यता की जांच

a = 6   b = -7     c = -3

शून्यको का योग (α+β)=   -b/a

(-⅓  +3/2  ) = -(-7)/6

7/6 = 7/6

शून्यको का गुणनफल (αβ)=   c/a

-⅓*3/2= -3/6

-½=-½

दोनो स्थितियों में संबंध सत्य है

(iv)4u²+8u

हल:

4u(u+2)=0

अतः 4u=0और (u+2)=0

u=0 और u=-2

u का दो शून्यक α =0 और β= -2

शून्यको तथा गुणांको के बीच के संबंध की सत्यता की जांच

a = 4   b = 8     c =0

शून्यको का योग (α+β)=   -b/a

(0+ -2)=-8/4

-2=-2

शून्यको का गुणनफल (αβ)=   c/a

(0*-2)= 0/4

0=0

दोनो स्थितियों में संबंध सत्य है

(V)

दोनो स्थितियों में संबंध सत्य है

(VI) 3x²-x-4

दोनो स्थितियों में संबंध सत्य है

2.एक द्विघात बहुपद ज्ञात कीजिए जिसके शून्यको के योग तथा गुणनफल क्रमशः दी गई संख्याए हैं।

i.) ¼ ,-1

ii) √2, ⅓

iii) 0, √5

iv) 1,1

v) -¼ ,¼

vi) 4,1

Class 10 maths chapter 2 exercise 2.3

प्रश्नावली 2.3

1. विभाजन एल्गोरिथ्म का प्रयोग करके, निम्न मे p(x) को g (x) से भाग देने पर भागफल तथा शेषफल ज्ञात कीजिए:

1. p (x)=x³+5x-3, g(x)=x^2-2
2. p(x)=x⁴-3x²+4x+5, g(x)=x²+1-x
3. p(x)=x⁴-5x+6, g(x)=2-x²

(I) p(x)=x³+3×2+5x-3. g(x)=x^2-2

भागफल = x-3.    शेषफल=7x-9

(II) p(x)=x⁴-3x²+4x+5, g(x)=x²+1-x

भागफल = x²+x-3    शेषफल=8

(III) p(x)=x⁴-5x+6,  g(x)=2-x²

भागफल =- x²-2  शेषफल=-5x+10

2 . पहले बहुपद से दूसरे बहुपद को भाग करके, जांच कीजिए कि प्रथम बहुपद द्वितीय बहुपद का गुणनखंड हैं.

1. t²-3, 2t⁴+3t³-2t²-9t-12
2. x²+3x+1, 3x⁴+5x³-7x²+2x+2
3. x³-3x+1,x⁵-4x³+x²+3x+1

(I) t²-3, 2t⁴+3t³-2t²-9t-12

हल

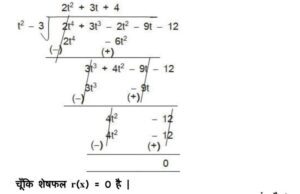
अतः t²-3, 2t⁴+3t³-2t²-9t-12 का एक गुणनखंड है

(ii) x²+3x+1, 3x⁴+5x³-7x²+2x+2

अतः x²+3x+1, 3x⁴+5x³-7x²+2x+2 का एक गुणनखंड है

 (iii) x³-3x+1,x⁵-4x³+x²+3x+1

अतः x³-3x+1,x⁵-4x³+x²+3x+1 का एक गुणनखंड नही हैं।

(3) 3x⁴+6x³-2x²-10x-5  के अन्य सभी शून्यक ज्ञात कीजिए यदि इसके दो शून्यक  √ 5/3    और -√5/3 है।

p(x)=3x⁴+6x³-2x²-10x-5

अब, 3x²-5 से 3x⁴+6x³-2x²-10x-5 मे भाग देने पर

अतः p(x)=(3x²-5)(x²+2x+1)

अब,x²+2x+1 को गुणनखंड कर शून्यक ज्ञात करने पर

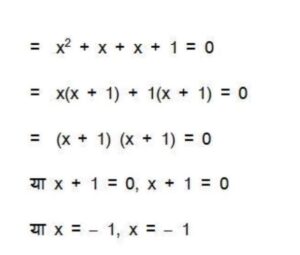
अतः अन्य दो शून्यक -1और -1 है

4)यदि x³-3x²+x+2 को एक बहुपद g(x) से भाग देने पर भागफल और शेषफल क्रमशः x – 2 और -2x+4 है तो g (x) ज्ञात कीजिए।

हल:

दिया है भाज्य:p (x)= x³-3x²+x+2

भगफल:  q(x) = x – 2

शेषफल:  r (x) = -2x+4

भाजक:   g(x) =?

भाज्य= भाजक ×भगफल + शेषफल

P(x)=q(x)g(x)+r(x)

x³-3x²+x+2 =g(x)(x – 2)+(-2x+4)

g(x)(x – 2)= x³ – 3x²+3x-2

अतः भजक g(x)=x²-x+1 है।

5)बहुपदों p ( x ) , g ( x ) , q ( x ) और r ( x ) के ऐसे उदाहरण दीजिए जो विभाजन एल्गोरिथम को संतुष्ट करते हों तथा

 ( i ) घात p ( x ) = घात q ( x ) हो

( ii ) घात q ( x ) = घात r ( x ) हो

 ( iii ) घात r ( x ) = 0 हो

युक्लिड विभाजन एल्गोरिथम से

p ( x ) = g ( x ) x q ( x ) + r ( x )

( i ) घात p ( x ) =घात q( x ) हो

हल :

भाज्य p ( x ) और भागफल q( x ) की घात सामान तभी हो सकता है जब भाजक g ( x) की घात 0 अर्थात कोई संख्या हो |

 उदाहरण : माना p ( x ) = 2x² – 6x + 3 और

 माना g ( x ) =2

भाग देने पर

p ( x ) = 2x² – 6x + 2 + 1 = 2 ( x² – 3x + 1 ) + 1

अब 2 ( x2 – 3x + 1 ) + 1 को p ( x ) = g ( x ) x q ( x ) + r ( x ) से तुलना करने पर हम पाते हैं :

अत : q ( x ) = x² – 3x + 1 और r ( x ) = 1

इससे घात p ( x ) = घात q ( x ) प्राप्त होता है |

 ( ii ) घात q ( x ) = घात r ( x) हो

 हल :

यह स्थिति तब आती है जब p ( x ) और g ( x ) का घात सामान हो जैसे –

माना

 p ( x ) = 2x² + 6x + 7 और g ( x ) = x² + 3x + 2

p(x)=2(x² + 3x + 3)+1

भाग देने पर :

q( x ) = 2 और r ( x) = 1

 अत : घात q( x ) = घात r ( x) है |

( ii ) घात r ( x ) =0 हो

 हल :

r ( x ) = 0 तब होता है

जब p ( x ) , g ( x ) से पूर्णत : विभाजित हो :

 P ( x ) = x² – 1 , g ( x ) = x + 1 विभाजित करने पर q q( x ) = x – 1 और r ( x ) = 0 प्राप्त होता है ।

Class 10 maths chapter 2 exercise 2.4

प्रश्नावली 2.4

1)सत्यापित कीजिए कि निम्न त्रिघात बहुपदों के साथ दी गई संख्याएँ उसकी शून्यक हैं । प्रत्येक स्थिति में शून्यांकों और गुणांकों के बीच संबंध को भी सत्यापित कीजिए :

( i )2x³ + x² – 5x + 2 ; ½ ,1 , -2

( ii ) x³-4x² + 5x -2 ; 2,1,1

हल  :

 ( i ) 2x³ + x² – 5x + 2 ; 2,1 , -2

माना p ( x ) = 2x³ + x²-5x +2  

इसलिए , p (½) = 2 (½ )³ + ( ½  ) -5 (½) +2

 = 2×⅛    + ¼  – 5×½   + 2

=  ¼ +¼  -5/2 +2

= 2/4 +2 -5/2

= ½ +2 -5/2

= 5/2  -5/2=0

इसलिए ½  p(x) का शून्यक है

 अब ,

 p ( 1 ) = 2 ( 1 ) ³ + ( 1 )²-5( 1 ) +2

= 2×1 + 1- 5 x 1 + 2

= 3-5 + 2 = 5-5 = 0

 इसलिए , 1 , p ( x ) का शून्यक है ।

अब ,

p ( -2 ) = 2( -2 )³ + ( -2 )² -5( -2 ) +2

= 2x ( -8 ) + 4 + 10 + 2

= -16 + 4 + 10 + 2 = -16 + 16 = 0

 इसलिए , -2 , p ( x ) का शून्यक है ।

 इसप्रकार , ½ , 1 और -2 , p ( x ) के शून्यका हैं ।

( ii )x³-4x² + 5x -2 -2 ; 2,1,1

हल  :

 माना p ( x ) = x³ – 4x² + 5x – 2

 इसलिए , p ( 2 ) = ( 2 )³ – 4( 2 )² + 5 ( 2 ) – 2

 = 8 – 16 + 10 -2

= 18 – 18 = 0

इसलिए , 2 , p ( x ) का शून्यक है ।

 अब , p ( 1 ) = ( 1 ) ³ – 4 ( 1 )²+ 5 ( 1 ) -2

 = 1-4 + 5-2 = 6-6 = 0

 इसलिए , 1 , p ( x ) का शून्यक है ।

इसप्रकार , 2 , 1 और 1 , p ( x ) के शून्यक हैं ।

2) एक त्रिघात बहुपद प्राप्त कीजिए जिसके शून्याकों का योग दो शून्याकों को एक साथ लेकर उनके गुणनफलों का योग तथा तीनों शून्याकों के गुणनफल क्रमशः 2 , -7 , -14 हों ।

3) यदि बहुपद x³ – 3x² + x + 1 के शून्यक  a – b , a ,  a + b हों , तो a और b ज्ञात कीजिए ।

हम जानते हैं कि ,

4)यदि बहुपद  x⁴ – 6x³ -26x²+ 13x – 35 के दो शून्यक 2 +√3 और 2-√3 हों , तो अन्य शून्यक ज्ञात कीजिए ।

 हल:

माना p ( x ) = x⁴ – 6x³ – 26x² + 13x – 35 दिया है

2 + √3 और 2 – √3 बहुपद p ( x ) के दो शून्यक हैं

इसलिए ,

 ( x – 2 – √3 ) और ( x – 2 + √3 ) बहुपद p ( x ) के दो गुणनखंड हैं

5)यदि बहुपद x⁴ – 6x³ + 16x² – 25x + 10 को एक अन्य बहुपद x² – 2x + k से भाग दिया जाए और शेषफल x + a आता हो , तो k तथा a ज्ञात कीजिए ।